Spamming you: project updates

So, I will start using this blog to report the advances on my research. It will as general as possible so anybody interested would be able to follow. I am doing this because I need to push myself to write everyday, and do closures after every milestone created. Giving that I am doing this only 5 months before my hand-in date, it can be a bit too late to inform you, but we will see how does it go.

Today I am going to ramble a bit on one of the open threads in my research

Open Specifications of Concurrent Processes. The most common way of specifying concurrent systems is to take a set of communicating processes, and establish the interactions between them by input-output primitives. Think for a second on a model in which you have a patient Alice, a doctor Bob, and a Social Worker Charlie (switch the gender of roles if you think I am being chauvinist here). Now, you will like to express a case in which the patient feels and comes to the doctor in order to receive a prescription.

The following set of activities will be included in our specification S:

1. Alice comes to Bob for a medical appointment.
2. Bob checks out on Alice and formulates a medicine treatment.
3. Bob sends the medicine formulation to Charlie, so he can deliver it to Alice.
4. Alice gets the medicine from Charlie and starts taking her treatment regularly as specified by Bob.
5. After some days, Alice comes back to Bob for a control, and the symptoms have dissapeared.

Now, many details have been hindered from this example. First of all, the current example only details the interaction between three of the main actors involved. This is, however, not a complete model. For instance, considering a private health care institution that has to fulfill auditing processes, we will have that, between phases 2 and 3. other actors will come into play.

Our specification S will be extended accordingly. We call the new model S´:

1. Alice comes to Bob for a medical appointment.
2. Bob checks out on Alice and formulates a medicine treatment.
3. 1. David, the accountant, has to certify that the treatment is covered by the insurance hired by Alice.
   2. Emma, has to Audit that the process is fulfilling the standards given by the healthcare institution with respect to prompt medicine delivery, quality of service and so on.
4. 1. Bob sends the medicine formulation to Charlie, so he can deliver it to Alice.
5. 1. Alice gets the medicine from Charlie and starts taking her treatment regularly as specified by Bob.
6. 1. After some days, Alice comes back to Bob for a control, and the symptoms have dissapeared.

So, here the question is: Is it S a valid specification? and How is S related to S'? Is it clear that the notion that we are looking for has a lot to do with refinement. Basically, refinement will tell us that a specification S and an implementation Q are related if the set of behaviors in S is a subset of the set of behaviors exhibited by Q. Up to here, there's nothing new to the concept, and you can simply google "refinement concurrency" and will find a lot of examples, most of them based in similarities and testing theories.

Now, most of the times we will start specifying systems constructively, adding up more and more roles (and their respective behaviors) over the time. This, will lead us to start with a specification like S, knowing that each of the actions can be further refined with more and more behavior. To do so, transitions in S can be either the classical, fixed ones where a process exhibits an immediate a before evolving into P', or can be "open" transitions 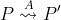, where the process P can exhibit a series of actions in A before evolving into P'. This "open transitions" allow us to describe explicit stages in a process in which a process can be refined with any of the actions considered. Here, transitions become weaker, as they might need more than one step for moving from P to P', they also become broader, as the set A can involve more than one action a.

Obviously, these changes lead us to a different notion of refinement, in which you consider sets of transitions instead of a single, hardcoded interaction. Without bothering you with the details, we will say that an open refinement relation P R Q considers 1) That the transitions in P are covered by the transitions in Q, and 2) That if P allows for a open transition of the form 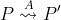, then there exists a sequence of transitions in from Q to Q' such that all actions in A are covered.

The new definition of open specifications lead us to very interesting paths on the verification of processes. First, open specifications are partial specifications by nature, and then one can explore the connection between these and logical reasoning. Returning to the example, one might be interested in saying things like "I know that I have to visit the doctor, and irrespective of all the other agents possibly involved, once I am in front of the social worker, he should deliver my medicine".

Currently, we already have the definitions of open specifications and refinement, plus a small logic to relate the transitions on a process and a set of formulae in the logic. Our next step is to map different specification models (for instance, the Pi calculus, or a Calculus for Choreographies) into this model, to prove its usability. My plan is to be able to talk a bit more on this subject from here until the beginning of October.